Larry Summers on China
Will China's growth slow? Overrated-Underrated on SOEs, industrial policy, the China Card, and Wolf Warrior diplomacy. Plus, how should US academia relate to a changing China?
The following is a transcript of a podcast I recorded with Larry Summers last week. Dr. Summers is a professor at Harvard, and previously served as Clinton’s secretary of the treasury and Obama’s national economic director. Co-hosting with me was Logan Wright, Director for China Markets Research at Rhodium.
Overrated-Underrated on SOEs, Industrial Policy, The China Card, Wolf Warrior Diplomacy, and American Democracy
Schneider: Overrated, underrated: state-owned enterprises.
Summers: Underrated in many cases. Some of them are actually state-of-the-art, successful, entrepreneurial in funding venture capital. There’s a tendency to see them in a bit overly ideological terms in the West.
Schneider: America pursuing industrial policy in the 2020s?
Summers: Currently excessively in fashion. We’re not going to be able to do it very well in many cases. The objectives are unattainable. Trying to raise (in a large-scale way) the fraction of American workers who were doing production work in manufacturing is futile for the same fundamental reason that trying to raise the fraction of people who work on farms is futile. There’s a tremendous productivity increase coupled with a relatively inelastic demand.
Schneider: Using China as your main way to politically drive domestic regulation.
Summers: Overrated. Declaring enmities can too easily become a self-fulfilling prophecy. I’m comfortable with advocacy that suggests that we’re very much engaged in a global struggle where the power of our example is going to be essential. But where it is suggested that we need to pursue certain kinds of domestic policies in order to confront an adversary, I worry about the internationally polarizing consequences of that approach.
Schneider: Wolf warrior diplomacy.
Summers: I think it’s a grave problem. I think that for those of us who believe that the major problems of the 21st century are issues like climate change, global health and pandemic risk ... for those of us who see those challenges as central, we also see being able to cooperate with China as central in meeting them. We would therefore like to see our relationship with China more oriented toward cooperation on those issues than on ideological point-scoring having to do with political issues. Wolf warrior diplomacy, because of the outrageous things that are said, renders fostering cooperation much more difficult. So I think it’s very pernicious.
Schneider: And we got a big one to close: America’s political system.
Summers: I think it’s underrated. I think that the lesson of American history is a lesson of self-denying prophecy: that John Kennedy believed that Russia was surpassing us; that at the end of the Carter administration it was generally believed that we were suffering a malaise and our constitution might need to be amended; that many believed and suggested that Roosevelt needed to take dictatorial powers in 1932; that in 1792, Patrick Henry said that the spirit of the revolution had already been lost.
I think the narrative of American history is the American people’s and their leaders’ capacity for alarm and for that alarm to lead to renewal and rejuvenation. I think that is the process that is being set in motion right now. So I am ultimately an optimist about the United States.
I believe Winston Churchill did not actually say what is often attributed to him, but I do believe the statement is correct that America tends to do the right thing, but only after exhausting the alternatives. And I think in many areas, people will look back at this moment and that’s what they’ll see.
Schneider: One last one because I can’t help myself: What are your biggest outstanding analytical questions about China that you’d love to learn more about or try to get answered?
Summers: I’d like to understand the questions around the demographic changes that China is going through, both the obvious in terms of a declining labor force, but also the less obvious in terms of the consequences of rural-to-urban migration of those who can be productive in urban areas being largely exhausted.
I’d like to better understand how China has nurtured a cutting-edge set of venture-type companies despite being a relatively poor country. I’d like to understand better the questions of a transition of power and the possibilities of wrenching change from the current system in China. History tells me that protracted continuity for fifty years is unlikely, but I don’t have a good feeling for its likely discontinuity.
And I’d like to understand better the attitudes of ordinary Chinese people towards the United States and towards the rest of the world, because I think it is a mistake to assume that authoritarian states are not responsive to the popular will. Often authoritarians who lack the legitimacy of democratic election have even more need to cater to the popular will in order to maintain power. So understanding the weltanschauung of Chinese citizens towards the rest of the world seems to me profoundly important.
Schneider: I guess I have the agenda for the second half of 2021 ChinaTalk episodes.
Favorite Bureaucracies and Why China Lost Faith in the West
Schneider: Is there a historical bureaucracy you’d really like to have been a fly on the wall for or to have worked in?
Summers: I’d have liked to have seen what it was like when the Marshall Plan was being conceived and implemented, because I think that was the most profound success of economic foreign policy that the world has ever seen.
I would have also liked to be a fly on the wall in the early years of Chinese economic reform planning, after Deng Xiaoping effectively took power in 1979.
From a very different perspective, I’d liked to have been present in the foreign ministries of Europe in the thirty-nine days before World War I, so that I could better learn the negative lessons that were to be learned from that experience.
Schneider: Let’s stick with Chinese economic policymaking. How has your estimation of China’s policymaking changed since Deng?
Summers: I think for better or for worse—and it’s some combination—China has become less receptive to Western influence. I think the China of the 1990s was a China that believed that a great deal of economic wisdom was present in the West. It believed in the remarkable power of markets, was more open to the idea that free societies and free markets were things that went together.
Three things have probably contributed to some substantial loss of admiration for Western economic practices or respect for the American capitalist example. I think that it’s always the case that as young people succeed and gain strength, they become more determined to set their own path rather than to follow the path of those who have gone before. And as Chinese incomes increased manyfold between 1990 and 2010, China became more confident in its ways.
The second thing that happened was this: for those who thought the West had it all figured out, the combination of the 2009 financial crisis, the election of Donald Trump, and the failure in initially containing Covid-19 just gave less of the sense that this was a place to learn how to architect a society.
And I think the third thing is that the rising tension and sense of competition between the West and China inevitably led to an emphasis, in China, on defining its own greatness in its own way.
For all these reasons, I think Chinese economic policymaking has become more distinctively Chinese and less an evolution towards models akin to those of the United States or Europe.
Another piece of this is a big change in thinking—of a kind which I certainly did not foresee—about the relationship between information technology and political openness. I was very given, in the early1990s, to remarking on the fact that during the 1980s countries like the United States or Japan or the UK had many more telephones than televisions—perhaps three times as many telephones as televisions. But in Russia, there were twice as many televisions as there were telephones. And my explanation for that had to do with a preference for one-way communication over two-way communication.
It was my belief during that period that some of the success of the much-derided Star Wars strategy came from the fact that delivering the kind of information technology that was necessary to compete was inconsistent with being a completely closed society in the way that Russia was.
I did not anticipate the ways in which information technology—through things like social-credit mechanisms and the ability to monitor and manage social networks—can be reinforcing of authoritarian models rather than undermining of authoritarian models. But it is probably important in terms of understanding the current architecture of economic competition.
How Harvard Should Handle China
Schneider: There are lots of recently retired or current senior officials of the CCP who’ve spent a month hanging out at HKS, and I feel like the next generation are probably not going to have that on their résumé, both because the CCP is warier and wants to learn less from the West, as well as some fundamental challenges that are wracking American academia as they think about engaging with the Chinese government and mainlanders in general. How do you think that American universities should think about navigating this relationship?
Summers: I think it’s a very profound question. When I was president of Harvard, it was my general view that American universities needed to remember that they were in a sense institutional citizens of the United States. I was appalled by Harvard’s policy, for example, on ROTC. I yield to no one in the strength of my conviction in gay marriage, but I did not think it was appropriate for Harvard to refuse to be part of ROTC because it didn’t like the policies of our elected officials in that realm.
I was also sympathetic to the idea that, under certain circumstances, law enforcement to prevent terrorist incidents, with appropriate search warrants, might need to have access to academic records.
So I think it is reasonable to ask American universities to be concerned with American interests. At the same time, I think we need to be very careful about the ways in which we limit interchange and interconnection.
Two stories about American universities and the former Soviet Union have always stayed with me. One has to do with a man named Alexander Yakovlev. He functioned as Gorbachev’s ideological adviser, and it is widely believed that he was the progenitor of the terms perestroika and glasnost. When he was asked, “Where did this all come from? Where did you, a long time party apparatchik, come forward with these concepts?,” he referred to the year he had spent in the late 1950s in Columbia University’s political science department and all that he had seen in the United States. This all deeply affected his thinking. And I thought to myself that whatever program paid for that—
Schneider: —is worth more than Star Wars.
Summers: Absolutely.
The other story, which is a bit closer to home for me, was some years ago there was a Russian submarine that was sitting on the ocean floor that needed to be rescued. All aboard would perish if it was not rescued.
The reason it was ultimately rescued was that Russian admirals on the submarine had attended a program at the Kennedy School that brought together naval officers from the US and the Soviet Union. So they knew each other and had a personal rapport that enabled them to be in touch with each other to make that rescue possible. That program increased, for a time at least, the extent of goodwill between the countries.
I’ve certainly heard stories of influence activities by Chinese authorities in American universities, and it seems to me we can’t tolerate this and need to be very attentive. But I think we would make a serious mistake of the national interest to avoid American universities engaging with Chinese students and Chinese scholars.
But I think it’s entirely right that questions be asked. And I think when universities say that the idea of export controls is something that should be applied to companies but not to universities as a matter of absolute principle ... I don’t actually think that’s a tenable position.
So I think there’s a scope for a lot of thinking within the American academy about these questions.
Secular Stagnation in China
Wright: Obviously we’re aware you’ve been heavily involved in the debate over US economic conditions, but we wanted to ask your thoughts about how those theories apply to China’s economy as well. Let’s start with secular stagnation. How does the secular stagnation argument apply in your view to China’s economy? Is it different from conditions in developed economies, or are the same forces fundamentally at work?
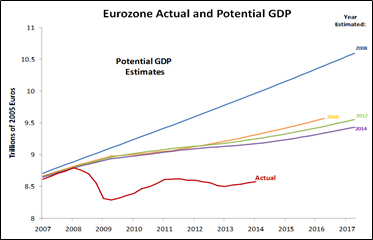
Ten years of secular stagnation in the Eurozone [Source]
Summers: I think it’s odd to apply the concept of secular stagnation in the form that I have talked about it to an economy that’s grown more rapidly than almost any other economy in the world. On the other hand, I think the issues pointed out by the secular-stagnation theory are very relevant to China.
What secular stagnation directs attention to is the question of how an economy absorbs saving. In the American context, or the industrial-world context at large, secular stagnation is basically a concern that private saving is excessive relative to the demand for private investment, even at very low interest rates.
As a consequence, you have very low interest rates, shortfalls in demand, and a tendency to asset bubbles because those saving flow into existing assets. The way that has manifested itself in China over time, which has an extraordinary savings rate, is increased pressure to absorb all of that saving.
And that pressure to absorb saving has a central economic problem, which is what defined secular stagnation, has defined two aspects of the Chinese experience over time: it has defined the enormous emphasis on public investment and infrastructure investment. It’s basically the avoidance of secular stagnation that explains why in four years of the previous decade, China laid more concrete than the United States did in the entirety of the 20th century.
So the first way in which secular stagnation theory explains Chinese performance is it points to those very high levels of public investment. It also explains the pattern of China’s international accounts. One might normally expect that a country that had tremendous growth prospects, that was industrializing extremely rapidly, that was seeing vast labor exit from rural agriculture, would be a country that would be importing capital on a substantial scale. But the level of saving in China is so great that it actually has been exporting capital on a substantial scale, particularly up to the last several years.
That savings absorption problem is the key to understanding the mercantile tendency in Chinese policy. If there had been an open capital market, it might not have been mercantile policy, it might simply have been substantial capital outflows coupled with a relatively weak exchange rate. In the presence of capital outflow controls, however, it manifests itself in a mercantile approach directed at maintaining the level of demand. The logic of secular stagnation theory helps to explain two of the very striking characteristics of Chinese economic performance.
In a way there’s a resemblance between China in the first part of the 21st century and Britain at the end of the 19th century. In both cases, there were substantial pressures for saving that led to very substantial external investment. Some of the economics of the British Empire parallel some of the economics of belt and road.
Is Chinese Mercantilism a Global Problem?
Wright: Over the course of the pandemic, we’ve seen a huge expansion in China’s current account surplus, with that surplus of savings over investment as a continuation of this mercantilist behavior. We can compare China’s stimulus efforts to those of developed economies.
Is the persistence of that current account surplus a concern, and if so, how much of a concern should it be to developed economies, particularly the United States attempting to create a more sustainable post-pandemic recovery.
Summers: From a global point of view, saving absorption is a problem. That’s why we are living in a deflationary era (in most places outside the United States, that is). That’s why the world economy is currently defined by extraordinarily low real interest rates.
From that point of view, what is problematic is China’s decision to focus less on the promotion of domestic demand and more on the promotion of exports, and the decision to not take bold and dramatic steps to lift the share of consumption in GDP. To the extent that one believes that the liquidity trap, the zero lower bound, and extremely low neutral real interest rates are different words for a similar phenomenon involving an excess of savings ... if China were reducing its level of domestic saving or doing more to channel that domestic saving into investment, those would be smaller problems in the global economy.
Wright: At the same time, we’ve seen this phenomenon where the Chinese financial system has been less efficient over time at intermediating savings into investment. So we can see different sorts of concerns.
On the one hand, you have a financial system that’s expanded very fast relative to the size of its economy overall, which could lead to financial spillovers if credit growth continued at that pace. On the other hand, we have this idea that even if China did stimulate investment, it still might not necessarily reduce the current account surplus over time.
Which of these concerns is bigger for developed economies?
Summers: I’m not sure I completely share your indictment of the Chinese financial system. The fact that China has cutting-edge technology companies in as many areas as it does despite having 25 percent of US per capita income and PPP and probably 18 percent at exchange rate measures can be attributed to the fact that the finance-entrepreneurship ecosystem in China is doing something very valuable. The fact that China has been more successful in the field of software than Europe has is some kind of positive reflection of what’s going on in China.
It’s not my impression that all those investments are being made by the public sector—many are being made by a flourishing venture capital industry. So I think one has to be careful in condemning everything in Chinese finance. I do think that it’s probably the case that there are many continuing instances of financial repression in China, and that does lead to a fair amount of investment channeled into relatively efficient uses.
That may catch up with China at some point. That’s one of the suspicions I have as to how the mean reversion, which I’ve worried about with respect to China, will manifest itself.
Is Chinese Growth Mean Reversion Inevitable?
Wright: I wanted to ask you about the paper you wrote in 2014 with Lant Pritchett on mean reversion. What we found interesting was the argument that continuity of growth should not really be the prevailing assumption. The more dominant characteristic in history was this reversion to the global mean growth rate. In that context, are there still good arguments in your view why China’s growth should deviate from the global mean growth?
Summers: I suspect that a fair-minded Chinese observer could legitimately have a bit of an I-told-you-so moment with respect to what we wrote, in that Chinese growth has reverted towards a global mean less rapidly than we had supposed might be the case.
I think we were always careful to frame our analysis as a statistical tendency rather than as an iron law. I think the rather disappointing performance of India in the last few years, which was something we also predicted, means that as predictors the relationships that Pritchett and I applauded look a bit more realistic.
It’s always very hard to know about Chinese growth. It’s clear that there is enormous technological capacity, enormous entrepreneurial potential, enormous capacity for hard work in China. It’s also clear that there are substantial demographic headwinds, that there are substantial environmental headwinds, and that there are substantial issues of political economy.
On the one hand, the maintenance of loyalty to the Communist Party is seen as essential, and the selective dispensation of favors is the best-known way that mankind has to maintain loyalty, whether it’s Tammany Hall in turn-of-century New York or whether it’s the Chinese Communist Party.
On the other hand, corruption, which is very much like the selective dispensation of favors, is inimical to legitimacy, and the eradication of corruption was a very focal point of the early years of Premier Xi’s rule.
So I think it’s very difficult to know. My own suspicion is that while it is hard to call the timing with precision and while it may not apply to every sector, in the same way that the Kennedy era’s fears about Russia surpassing us look silly today, and the same way the profound alarm in the 1980s that the Cold War was over and Japan won today looks silly, I think that some of the more overheated views of China as an economic threat to the United States and some of the more dramatic projections of continued extraordinarily rapid Chinese growth look excessive.
Schneider: So will it take a financial crisis for the world to recorrect its assumptions about the future Chinese trajectory? What happens once the world realizes we’re not in a Japan 1980 scenario?
Summers: I’m not sure what the answer to that is. I can imagine scenarios that have the character of changed assessments of the Soviet Union, where there was no discontinuous event. Rather, there was the exaggeration of initial success followed by decay of performance, followed by belated recognition. There was no dramatic moment.
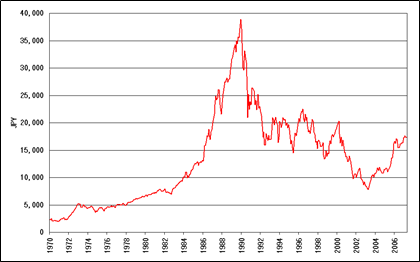
In the case of Japan, people felt that the most bubbling market was Japan. The prevailing position of people who played in markets was this: short Japan, long the rest of the world. The 1987 crash happened and Japan was more insulated from the crash than other countries—its markets recovered more rapidly than other countries. Two years later, the Japanese bubble burst. That was not just a financial event, but a sign of a kind of profound change in growth in prospects of Japan, which took years to be fully recognized. The Nikkei peaked in late 1989, and the early Clinton administration at the beginning of 1993 was in high alarm about Japan, and took it just about as a given that the Japanese productivity growth rate would significantly exceed the American productivity growth rate.
Nikkei stock average, 1940–2015 [Source]
I think these things are likely to take time, and I would not expect some kind of seismic collapse in China that shakes the world. I would expect that historians will look back and find that the current view of Chinese economic prospects to have been overly benign in important respects.
But let me say that’s just my best guess, but it’s not a view I hold with anything like complete confidence. The degree of shiny strength—the variety of cutting-edge technology in particular—gives me some pause in making these judgments.


Excellent interview Jordan!
(1) Worth bringing up a more nuanced view of China's GDP per capita than the average of 18-25% that of the United States cited. Urban centers and coastal provinces may be around half the GDP per capita and have quite high technological proliferation, while poorer in-land provinces and rural areas bring down the average. In some ways it hearkens back the U.S. 100 years ago with vibrant Northern industry & poorer Southern states. The distinction is important because it helps explain why so many sophisticated tech companies are coming out of the more technologically advanced regions. It is also easier for a region to “catch up” when it is within the same country and speaks the same language - a la East Germany after reunification.
(2) China has certain industries in which it is already ahead of the West - e.g., e-commerce / logistics, payments (where the tax from WeChat / Alipay is a fraction the tax set by the duopoly Visa / Mastercard). The U.S. still wins in B2B software (for now) given a higher cost of labor and the benefits from automation, but I would expect this to change as the cost of labor increases in China and hungry Chinese entrepreneurs work 6 days a week building software businesses.
(3) Interesting to consider the role that American-trained VCs and investors have played in the rise of the Chinese tech sector. American universities have also played a major role. For example, Hillhouse Capital is named after a street of Jordan's alma mater Yale, and the founder received his training from the great Peter Swensen of the Yale Endowment. I would expect the U.S. to be more restrictive in the transfer of intellectual know-how on U.S.-trained tech firms & tech investors as the U.S. - China relationship evolves to become more rivalrous.
(4) Loved the narrative about the submarines. Let's not forget that Xi sent his daughter to Harvard. Hopefully personal relationships & respect can prevent a catastrophic "The Guns of August" WW1 scenario and keep both countries focused on working together on areas of mutual benefit.
A few points.
1. His comments vis-a-vis China and Europe in tech shows he doesn't understand technology. The main reason why Europe lags behind is because it isn't a unified market. As an economist, he should know this. Most IT services are just that -- services. And trade in services across European borders (even within the Schengen alone) is far more restrictive than in goods. There are good political economy reasons for this; Germany is much stronger in goods exports than in services.
Spotify's CEO noted that it was easier to expand to the US than to Spain from Sweden when they were a smaller company, despite Spain and Sweden both being in the EU. That should tell you much. So China's tech performance is simply a function of a completely unified market, and has nothing to do with their financial sector per se.
2. I agree that China's GDP prospects are likely exaggerated, but I think the biggest threat is not Chinese overperformance but rather internal dysfunction and disunity within the US. From someone who is neither American nor Chinese, it is the USA which looks far shakier internally. This isn't just a function of the US being a pseudo-democracy; public polls by American organisations like Gallup has consistently shown a much greater percentage of Chinese being happy with the direction of the country, while the opposite is true for Americans.